SEGITIGA

A. Pengertian Segitiga

          Segitiga adalah bangun datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik         sudut. Segitiga merupakan bangun datar yang dibuat dari tiga sisi yang berupa garis lurus yang saling           saling berpotongan dan tiga sudut yang tidak segaris. Jumlah ketiga sudut suatu segitiga ialah 180°. 

B. Jenis-jenis Segitiga

             Jenis-jenis segitiga ditinjau berdasarkan panjang sisinya, antara lain adalah sebagai berikut:

     1. Segitiga Sembarang

                  Segitiga sembarang adalah segitiga yang sisi-sisinya tidak sama panjang.

3        2. Segitiga sama kaki

            Segitiga sama kaki adalah segitiga yang mempunyai dua buah sisi sama panjang

     3. Segitiga sama sisi

            Segitiga sama sisi adalah segitiga yang memiliki tiga buah sisi sama panjang dan tiga                  buah sudut sama besar.

             Jenis-jenis segitiga ditinjau berdasarkan besar sudutnya, antara lain adalah sebagai berikut:

    1. Segitiga lancip

            Segitiga lancip adalah segitiga yang ketiga sudutnya merupakan sudut lancip, sehingga

        sudut-sudut yang terdapat pada segitiga tersebut besarnya antara 0o

        dan 90o. 

    2. Segitiga tumpul

                  Segitiga tumpul adalah segitiga yang salah satu sudutnya merupakan sudut tumpul. 

          3. Segitiga siku-siku

            Segitiga siku-siku adalah segitiga yang salah satu sudutnya merupakan sudut siku-siku
        (besarnya 90o)

            Jenis-jenis segitiga ditinjau berdasarkan panjang sisi dan besar sudutnya, antara lain adalah          sebagai berikut:

    1. Segitiga siku-siku sama kaki

            Segitiga siku-siku sama kaki adalah segitiga yang salah satu sudutnya 90o dan dua sisinya             sama panjang. 

    2. Segitga tumpul sama kaki 

           Segitiga tumpul sama kaki adalah segitiga yang salah satu sudutnya tumpul dan panjang           kedua sisinya sama.

    3. Segitiga lancip sama kaki

           Segitiga lancip sama kaki adalah segitiga yang salah satu sudutnya lancip dan panjang             kedua sisinya sama.

C. Keliling dan Luas Segitiga

     1. Keliling Segitiga

              Keliling segitiga adalah jumlah panjang ketiga sisi yang membentuk jumlahpanjang                  segitiga. K = sisi 1 + sisi 2 + sisi 3

        Contoh 1:

        Keliling sebuah segitiga 22 Cm. Jika panjang dua buah sisinya 8 dm dan 5 dm, berapakah panjang          satu sisi lainnya?

        Penyelesaian:

        Keliling segitiga adalah 

               K = Sisi 1 + Sisi 2 + Sisi 3
       20 cm = 8 cm + 5 cm + Sisi 3
       20 cm = 13 cm + Sisi 3
       Sisi 3 = 22 dm – 13 dm = 7 cm
      Jadi, panjang satu sisi lainnya tersebut adalah 7 cm.

  2. Luas Segitiga

      Perhatikan gambar berikut.

     

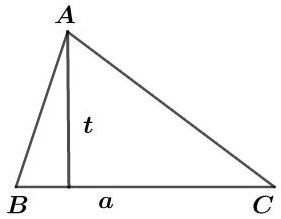
      Luas segitiga dirumuskan sebagai berikut.

                           L = ½ x a x t

  

RELASI DAN FUNGSI

RELASI

A. Pengertian Relasi

           Suatu relasi dari kelompok A ke kelompok B adalah memasangkan anggota-anggota                     kelompok A dengan anggota kelompok B. Relasi dari A ke B dituliskan dengan R : A —> B.

     Misalnya :

     3 “faktor dari” 12          ⇨         Hubungan “faktor dari”

     7 “lebih dari” 3                               dan “lebih dari”   

                                                             disebut  relasi (R)

B. Menyatakan Relasi

         Relasi dapat dinyatakan dengan 3 cara yaitu :

   1. Diagram Panah

   2. Grafik Cartesius

   3. Himpunan Pasangan Berurutan

    Contoh 1 :

    Misalkan ada dua himpunan A dan B dengan

           A = { 2, 3, 5 }

           B = { 3, 4, 5, 6 }

    Tunukkanlah relasi “faktor dari” dari himpunan A ke B dengan :

    a) Diagram panah

    b) Himpunan pasangan berurutan

    c) Koordinat Cartesius

    Penyelesaian :

    a) Diagram Panah 

       A     faktor dari    B  

      2      →     4 & 6

     3      →     3 & 6

     5      →     5          

    Pada relasi tersebut dapat dinyatakan hal-  hal berikut :

           2 adalah faktor dari 4 dan 6

           3 adalah faktor dari 3 dan 6

           5 adalah faktor dari 5

    b) Himpunan pasangan berurutan

          { (2,4), (2,6), (3,3), (3,6), (5,5) }

    c) Koordinat Cartesius  

     

FUNGSI

A. Pengertian Fungsi

            Suatu fungsi dari himpunan A ke B adalah hubungan dari A ke B dimana untuk setiap x € A           dipasangkan dengan tepat satu y € B. Jika x € A, y € B serta x  dipasangkan dengan dengan y,               maka y dinamakan bayangan atau peta dari x

B. Istilah-istilah pada fungsi

     1. Domain

     2. Kodomain

     3. Range

C. Notasi Suatu Fungsi

     1. Misalkan fungsi A ke B kita sebut f maka notasi yang digunakan untuk menyatakan fungsi itu adalah :

                                                      f : A → B

    2. Jika x € A, y € B, dan y adalah peta (bayangan) dari x maka notasi fungsi di atas ditulis sebagai berikut :

                                         f : x → y

        Penulisan di atas dibaca “fungsi f memetakan x ke y”.

    Contoh soal :

    1. Jika f(x) = x^2 – 4x, tentukan f(x-3)

    

    Penyelesaian : 

    f(x)    = x^2-4x

    f(x-3) = (x-3)^2) – 4 (x-3)                                                 (substitusikan (x-3) ke x

    f(x-3) = x^2 – 6x + 9 – 4x + 12                                         (penjabaran)

    f(x-3) = x^2 – 10x + 21                                                     (penyederhanaan)

PERKAWANAN (KORESPONDENSI) SATU-SATU

         Dua himpunan A dan B dikatakan dalam keadaan perkawanan (korespondensi)satu-satu apabila       anggota-anggota himpunan A dan B dapat dipasangkan sedemikian sehingga setiap anggota A             berpasangan dengan satu anggota B, dan setiap anggota B berpasangan dengan satu anggota A.

     Contoh soal :

     1. Suatu fungsi ditentukan dengan formula f(x) = x^3 dengan x € { 1, 2, 3 }

         a) Nyatakan fungsi itu dengan diagram panah.

         b) Nyatakan fungsi itu dengan himpunan pasangan berurutan.

         c) Apakah fungsi itu merupakan korespondesi satu-satu?

     Penyelesaian :

     a) Mula-mula kita buat tabel berikut ini :      

x	1	2	3
f(x)	1	8	27

                             Diagram panah

                                   A  f  B

                               1    →   1

                        2    →   8

                         3    →   27

      b) Himpunan pasangan berurutan :

                {(1,1), (2,8), (3,27)}

      c) Merupakan korespondensi satu-satu

Tonton juga video Youtube saya dengan mengklik link di bawah ini
https://youtu.be/m94p4f6CrAo